Reflections

The Number Corner

| Janaki Nagarajan

I’m not quite sure how I’ve managed to end up in this very specific situation twice thus far in my fairly short career, but here we are. (For context, here is my post from 4 years ago).

The Beginning (redux)

Slightly too accurate school bathroom decor

It was a Thursday when I learned I would take over as a 3rd grade teacher for the rest of the school year for a teacher who was going on maternity leave. On a Wednesday, a few weeks later, I was assigned to the school as a substitute paraeducator, and at noon, very unexpectedly, was told okay, it’s happening, and you’re the teacher now. There was some back and forth on whether this was actually true, whether the teacher would return for a couple more days, but come 11pm that night, it was clear *I* was now in charge of this class. While a global pandemic did not shut down our schools the next day, as it did the last time I was in this situation, I still felt far from entirely prepared.

All that to say – this past year (and especially past week) has been a whirlwind.

That first half day, going in with absolutely no idea what I was supposed to teach, was an interesting ride, to say the least. Following the general plans as best I could, trying my best to keep a handle on what I’d been told over and over was a very challenging class, I saw that the one academic routine that had been planned for that afternoon was the “Number Corner”.

The Corner of Numbers

Literally, numbers (kind of?) in a corner

I wasn’t super familiar with this routine, which is part of the Bridges in Mathematics curriculum – I had come across it a few times as I subbed across the district, though I spent most of this year teaching & subbing in the subset of schools in this district that use Illustrative Mathematics instead – so again, my understanding was something like – “there’s a calendar with patterns”.

I’m not going to claim to know much more about the idea of Number Corner than that in this post either – this story is really about eliciting and marveling at kids’ mathematical thinking.

Anyway, back to the story. I told the students it was time for Number Corner, and watched as they all filed into this little corner of the room – some on the floor, some standing behind, some at desks in the vicinity. And then I stepped back to watch them communicate their ideas – the excitement behind the patterns they noticed both in the visual representations on the calendar and the numerical ones on the chart (they hadn’t done it in a few days due to testing, so they were turning around quite a few of the squares).

And so, for a brief moment in the middle of a very, very hectic day, I got to listen to my favorite thing – kids’ thinking about math.

What happened Next

That afternoon, as I was debriefing my day with the principal (and trying to come up with a plan for the next one), she mentioned that the kids had been really engaged in the “math thing” we were doing (she had been in the class watching as we did this routine). At the time, I hadn’t given it much thought – it was on the schedule, I tried my best, kids seemed to enjoy it, but my understanding was that this routine was usually just a quick blip in the day, and sometimes skipped altogether.

It made me think though – what if I approached this routine with more intention? What would I find?

Sometimes, as teachers, we have things that we do in our classrooms because we love them so much, and they give us something in our days/weeks/months to look forward to. For me, that’s always been both “free art with interesting materials” and “free mathematics with interesting materials”. While this doesn’t quite fall into the latter category, “opportunities to see what kids think about math” is definitely a close second.

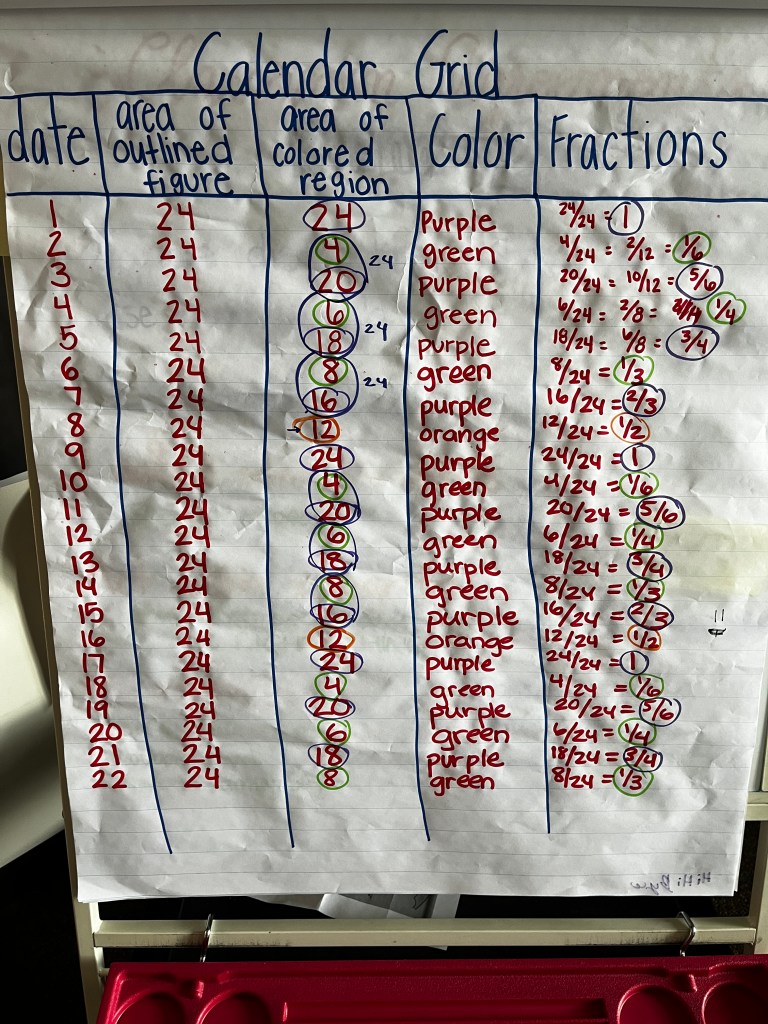
So then, what did they notice? A student I’d struggled to connect with immediately offered her prediction of a cyclical pattern with the fractions (we hadn’t reached the end of the first ‘cycle’ yet). The shock that came with the uncovering of the first orange shape was palpable. There was a lot of conversation attempting to predict when the next orange shape would come – some students thought that every 8 days, there would be a new color introduced. In the days to come, students noticed that the diagonals could be used to predict color and fractions, that every two days the total area added up to 24 (minus a couple outliers), and imagined how the outline of the shape might be manipulated in future dates to preserve the area of 24.

My favorite part is that during this time I can step back, listen, and facilitate/probe when necessary, but otherwise, the students have got it. They’re building on each other’s ideas, calling on each other, turning and talking, and are absolutely devastated if we have to wrap it up before they get a chance to share their idea.

What I’ve found particularly fascinating is that students, as a whole, have been significantly more engaged in our number corner routine than any math lesson we’ve done together* – even with lessons that are meant to be “hands on”, “exploratory”, or “fun”.

*Sidebar to say, they also did love when we played Illustrative Mathematics’ “Mystery Quadrilateral”.

To me, at least, this is a very interesting issue – and I’ll come back to it again in the next section.

For the days remaining in May, I’ve thought about how this routine they’ve already bought into can facilitate further mathematical thinking. Building off this as a warm up or cool down in math, thinking about the possibilities for the next new shape that will appear? Look more closely at the data we’ve collected for new patterns we see? (I’ve been really curious if they’ll make the connection that green < 1/2, orange = 1/2, and purple > 1/2 – or if that’s even an important thing to notice). We’ve tried a few of those ideas, as documented below.

A student’s prediction for 5/21
Another prediction
Calendar grid updated with colors to highlight patterns
What possibilities are there for the next shape?

As much as I love being wildly creative in my math routines and lessons, digging deeper, thinking about what new ideas I can try out – it’s also important to step back and realize the power in kids being excited about the math they’re doing – and go from there.

the epilogue (i.e. some random, possibly connected thoughts)

I’ve been reading texts from two math-y authors lately – Is Math Real? by Eugenia Cheng and Ben Orlin’s series of Math with Bad Drawings books. Both authors offer their thoughts on how doing mathematics is quite different than doing mathematics in school. While that sentiment is not new to me, and I’ve certainly made attempts to consider what bringing more of “the approach to mathematics that actual mathematicians use” into my classrooms, there are a couple ideas they put forth that have really elegantly stretched and also simplified my thinking on the math we do in classrooms.

First, Dr. Cheng says that the crux of what mathematics is about, and what mathematicians actually do, is justification (p. 73). As she says, this is the difference between “what is 6 x 8?” and “why does 6 x 8 = 48?” I think students love this routine in part because it requires them to justify their ideas, rather than calculate (similar to a good Which One Doesn’t Belong?). Any task they’re given during class (via the curriculum) is generally asking them to calculate (and sometimes, as a sort of bonus, have some sort of justification for that calculation – but more along the lines of “make sure your answer is correct). I think it’s also a time for students to be able to meaningfully talk to each other about their math ideas in a decidedly non-evaluative and curious way.

Second, in the introduction of the book Math Games with Bad Drawings, Orlin writes that “the secret to our brilliance is that we never stop learning, and the secret to our learning is that we never stop playing.” (p. 11) During the Number Corner, I see students playing with ideas – making conjectures, justifying ideas, creating generalizations out of patterns.

I’m excited to see what June will bring.

The “Low Kids”

| Janaki Nagarajan

Disclaimer: this post refers to “low kids” and “high kids” as ways students are often talked about in schools. I hope as you read it, it’s clear that I am using these terms to describe how students are consistently categorized in narrow and dehumanizing ways, and that we as educators need to stop doing this – not only because it’s damaging but because it’s inaccurate.

I grew up thinking that intelligence, particularly in math, was both linear and elusive. On-demand fact recitation, no paper, fast and clever. Learn one thing first, and then the next. Your intelligence is reflected in above-average standardized test scores. That’s how you know you’re good at math. (By these standards, I was decidedly “mid”.)

Something about this fixed idea of smartness has never quite sat right with me, and I’ve always been drawn to ideas rather than performance – but truthfully, educators almost exclusively use these methods to categorize student achievement (the “whys” of that are complex and would take ages to unravel – but suffice it to say, this is how it goes). By now, I’m used to it, but it still makes my blood boil. Someone’s iReady score (sub in your standardized test) is the least interesting thing about them – even if the conversation is specifically about that student’s understanding of mathematics (or any subject).

Before school started, I did my customary go-around to my new students’ former teachers, excitedly sharing with them which kids from their class I get to work with this year.

“She’s sweet, but she’s really low,” said one student’s teacher from last year, without pause. (Blood boiling but biting my tongue – trying to tell myself it’s not this teacher’s fault, she’s part of a system that encourages this kind of categorization).

But what do you see in this photograph? 

Three days into the school year, these two students (who were labeled as essentially unable to understand grade-level mathematics) were tasked with counting a collection of objects. Every other group started counting by ones. These two decided on a “big rectangle”. Their instinct was to organize, prior to counting. A sense of how structure and patterns can be utilized to help us understand mathematics seems vital. Their low iReady scores do not reveal their aptitude to think this way. (Surprise?)

This year, as a math intervention, my grade level was told to create ability groups to meet with during small group time. While this is not my ideal teaching strategy, I began to think how these groups could serve as a humanizing and empowering experience for these students – capitalizing on their strengths, and nudging them to explore new grade-level content. Getting to work explicitly with students who may struggle to feel successful in mathematics – and giving them new ways to engage with it and show what they know is actually exciting.

One thing I discovered was that using Illustrative Mathematics’ resources in small group was a way to engage these students in mathematical inquiry and problem-based learning (because the absolute last thing we should be doing is gatekeeping that sort of thing for the “high kids”).

These two “low kids”, using an IM card sort, immediately began making connections between representations, situations and expressions. They worked together, collaboratively, bouncing ideas off of each other and defending their thinking. They were able to show that they understood the multiplication ideas they’d only been working on for a week.

Another opportunity we’ve had in our classroom this year is to engage in mathematical modeling. In the below example, students used a consensus board to attempt to figure out how many days our box of Ritz crackers would last our class for snack. They had to use information they knew (6 stacks in a box, 32 crackers in a stack), make some decisions (how many crackers should students get per day? How many students will eat crackers each day?) to attempt to find a solution.

The student whose work is represented on the bottom is one who was labeled “low” by other teachers at the school. What do you see? What I see is that she diligently represented each cracker in each stack to show exactly how many crackers we were working with. I see she made a decision about how many crackers each student would get per day (4). I see she got stuck thinking about how to incorporate the number of people eating crackers each day (most students did) and would benefit from a nudge to consider how she might show the crackers eaten by the class in one day.

To be clear – I think her work is phenomenal – equally as fascinating as the others in her group, who had their unique strategies and models, and their own places they got stuck.

And let’s talk about math quizzes.

My feelings about quizzes are mixed. Long opposed to most traditional assessments, this year what I’ve found is when used strategically, they can be a really interesting tool to uncover students’ understanding of the mathematics they’ve been learning. Some students might choose to complete their quiz independently – while I might ask others if they can show me their thinking about a question in a different way (especially if they’re struggling to represent their ideas on paper, and are hesitant to grab manipulatives).

What do you think this “low” student is doing?

He correctly represented his thinking on paper – he counted his grapes by ones and slightly miscounted – but when prompted to show his thinking with cubes, immediately realized he could count by 10s, physically moving the cubes to show what had and hadn’t been counted.

He then used his cubes to immediately solve the next question (which was more complex, and involved ideas such as measurement division that we hadn’t explicitly talked about at this point).

Another “low” student, when working one on one with him building and counting equal groups, would join his cubes together to make his groups, and then join the groups into one long unifix cube tower and count each cube. He meticulously recorded his answers to multiplication equations as he worked through the questions with only slight nudges from me.

If these students understand the mathematical concepts being discussed in class just as much as anyone else, why are they even labeled the “low kids”?

When a computer assessment is your primary way of determining someone’s aptitude, you’re going to be left with the impression that some in your class “can” and some “can’t”. And what about when a significant amount of your students who are scoring low are designated as multilingual learners? They are literally processing language differently than students whose primary method of communication since birth has been English. (Similar for students with learning disabilities).

As a result, they may struggle with reading English at the level that grade-level assessments assume competency in – be it with decoding, comprehension, and/or vocabulary – and when the majority of math tasks students encounter have a high cognitive load up front (read it, understand it, solve it), the barriers are built right in.

Reading comprehension is connected to mathematics only insofar as word problems are the primary source of determining mathematical understanding. Without multiple ways for students to access mathematics content, and multiple ways for teachers to assess it, certain students will always seem “low” while others seem “high”.

Beyond reading, the pedagogical structures of many math curricula (and if we’re really getting into it, school in general) simply aren’t developmentally appropriate for some students. Kids need different things! School systems lacking the ability to give a student an accommodation they need to show they can understand a concept should not be taken to mean “the student cannot understand the concept”.

Here are some questions I’m thinking and reflecting about:

  • Do we need to categorize students sometimes? It it even possible to categorize students in a humanizing way?
    • If yes, under what circumstances does it make sense to categorize students? When doesn’t it make sense? 
  • What kind of categories are helpful? How do we know?
  • I (and other teachers) have to teach a curriculum with fidelity. I have to give certain tests with fidelity. I have to show these tests to families, administrators, and coworkers, and decisions about these students are made as a result of these tests.
    • Given all that, how do we push back on labeling “low kids” and “high kids” (or sub your favorite euphemisms – “struggling learners”, “high fliers”)? 
  • How much of the change that needs to happen is about what we say – i.e. the words we use – vs. what we do – i.e. the structures, routines, and learning opportunities in our mathematics classroom?